Теория Жаркова листовой штамповки

Theory of Zharkov the sheet forming

Теория Жаркова листовой штамповки. Часть 1. Одноугловая гибка (Zharkov's theory of sheet forming. Part 1. Oneangular bending)

Теория Жаркова листовой штамповки. Часть 2. Двухугловая гибка без прижима заготовки (Zharkov's theory of sheet forming. Part 2. Two-angular bending without holder of blank)

Теория Жаркова листовой штамповки. Часть 3. Двухугловая гибка с прижимом заготовки (Zharkov's theory of sheet forming. Part 3. Two-angular bending with holder of blank)

Теория Жаркова листовой штамповки. Часть 4. Вытяжка осесимметричной детали без утонения стенки (Zharkov's theory of sheet forming. Part 4. Deep drawing the axesymmetrical detail without wall necking)

Теория Жаркова листовой штамповки. Часть 5. Вытяжка осесимметричной детали с утонением стенки с учётом анизотропии заготовки (Zharkov's theory of sheet forming. Part 5. Deep drawing the axesymmetrical detail with wall necking taking into account anisotropy of blank)

Теория Жаркова листовой штамповки. Часть 6. Вытяжка детали сложной формы (Zharkov's theory of sheet forming. Part 6. Deep drawing the complex detail)

Теория Жаркова листовой штамповки. Часть 7. Испытание и правка растяжением (Zharkov's theory of sheet forming. Part 7. Testing on tensile and stretching)

Теория Жаркова листовой штамповки анизотропных материалов. Часть 8. Методика построения диаграмм анизотропии и проектирования технологических процессов на примере вытяжки цилиндрических деталей (Zharkov's theory of sheet forming the anisotropic materials. Part 8. Technique of construction of anisotropy diagrams and designing the technological processes on example of deep drawing the cylindrical details)

Метод Жаркова В. А. построения диаграммы предельных деформаций листового материала

Method by Zharkov V. A. of construction of forming limit diagram of sheet material

Метод Жаркова В. А. относится к области теории и практики листовой штамповки, а в частности, к исследованию механических свойств листовых материалов для оценки их штампуемости как возможности получения пластических деформаций без разрушения листовой заготовки, полученной из листового материала, на формоизменяющих операциях листовой штамповки, а также для использования в CAD/CAE-системах (Computer-Aided-Design/Computer-Aided-Engineering-системах) при компьютерном моделировании и проектировании формоизменяющих операций листовой штамповки перед их внедрением в автомобильной и других отраслях промышленности.

Недостаток известных методов построения диаграммы предельных деформаций (ДПД) листового материала заключается в том, что требуется использование специального дорогостоящего оборудования и длительный срок проведения испытаний и построения ДПД.

Задача теории Жаркова В. А. состоит в снижении трудоёмкости, сроков и стоимости построения ДПД листовых материалов.

Задачу решают следующим образом. Для определения вероятности разрушения листовой заготовки на формоизменяющих операциях листовой штамповки, таких как вытяжка или формовка сложных деталей типа коробчатых или кузовных, растяжение или обтяжка листов, используют два критерия:

1) разрушение в результате деформаций: на каждом этапе деформирования листовой заготовки точки с координатами наименьшей главной деформации ε₂ и наибольшей главной деформации ε₁ для всех элементов листовой заготовки должны располагаться ниже ДПД листового материала ε₁=f(ε₂) с определённым запасом P_d пластичности по деформациям; при заданной абсциссе ε₂ принимают ординату ε₁ до ДПД за 1 или 100 %;

2) разрушение в результате напряжений: точки с координатами главных напряжений σ₁ и σ₂ должны располагаться ниже диаграммы предельных напряжений (ДПН) листового материала σ₁=f(σ₂) с определённым запасом P_s пластичности по напряжениям; ДПН строят с помощью ДПД по уравнениям связи между деформациями и напряжениями; ориентировочно, ДПН соответствует предельному эллипсу пластичности σ₁²−σ₁σ₂+σ₂²=σ_s².

Напряжение текучести σ_s в зависимости от интенсивности деформаций ε_i рассчитывают с учётом упрочнения заготовки по формуле Жаркова В. А. [7] (Жарков В. А. Моделирование в системе Marc обработки материалов в машиностроении. Часть 7. Испытание и правка растяжением. – Вестник машиностроения, 2013, № 3):

σ_s=σ_т+σ_в,tε_iⁿ,   

n=ln{1−σ_т/[σ_в(1+δ_р)]}/ln[ln(1+δ_р)], 

где предел текучести физический σ_т или вместо него предел текучести условный σ_0,2, временное сопротивление, иначе, предел прочности σ_в, истинный предел прочности σ_в,t=σ_в(1+δ_р) и относительное равномерное удлинение δ_р определяют по ГОСТ 11701-84 "Металлы. Методы испытаний на растяжение тонких листов и лент. Metals. Methods of tensile tests of thin sheets and strips".

ДПД строят экспериментально для каждой марки, категории вытяжки и толщины листового материала. На сетке прямоугольной системы координат в положительном и отрицательном направлениях оси абсцисс откладывают наименьшую главную деформацию ε₂=ln(l_min/l₀), в положительном направлении оси ординат – наибольшую главную деформацию ε₁=ln(l_max/l₀) элементов образца, полученного из листового материала, где l₀, l_min и l_max – начальный, наименьший и наибольший размеры ячейки делительной сетки, касающейся зоны локального утонения и/или разрушения образца. На сетке прямоугольной системы координат зона ε₂>0 соответствует двухосному растяжению элементов листового материала, ось ε₂=0 – плоской деформации, зона ε₂<0 – растяжению со сжатием.

Для построения ДПД требуются длительные дорогостоящие испытания на специальной испытательной машине, которая имеется только на крупных предприятиях, а производители поставляют листовой материал с нормативно-технической документацией без ДПД и с минимальным количеством механических свойств. Поэтому по данному методу строят ДПД на основе только одного стандартного свойства материала, а именно, относительного равномерного удлинения δ_р по ГОСТ 11701-84. Значение δ_р берут из нормативно-технической документации на листовой материал, а при отсутствии δ_р проводят только одно испытание на одноосное растяжение образца из листового материала по ГОСТ 11701-84 с целью определения только одного этого свойства δ_р.

Если для выбранного конструктором листового материала в нормативно-технической документации известно только относительное удлинение после разрыва δ по ГОСТ 11701-84, и не известно δ_р, а машина для испытания на растяжение образца из листового материала с целью определения δ_р отсутствует, то сначала для аналогичного по механическим свойствам листового материала с известными значениями δ_р и δ рассчитывают коэффициент C=δ/δ_р, а затем для выбранного конструктором листового материала рассчитывают δ_р =δ/C.

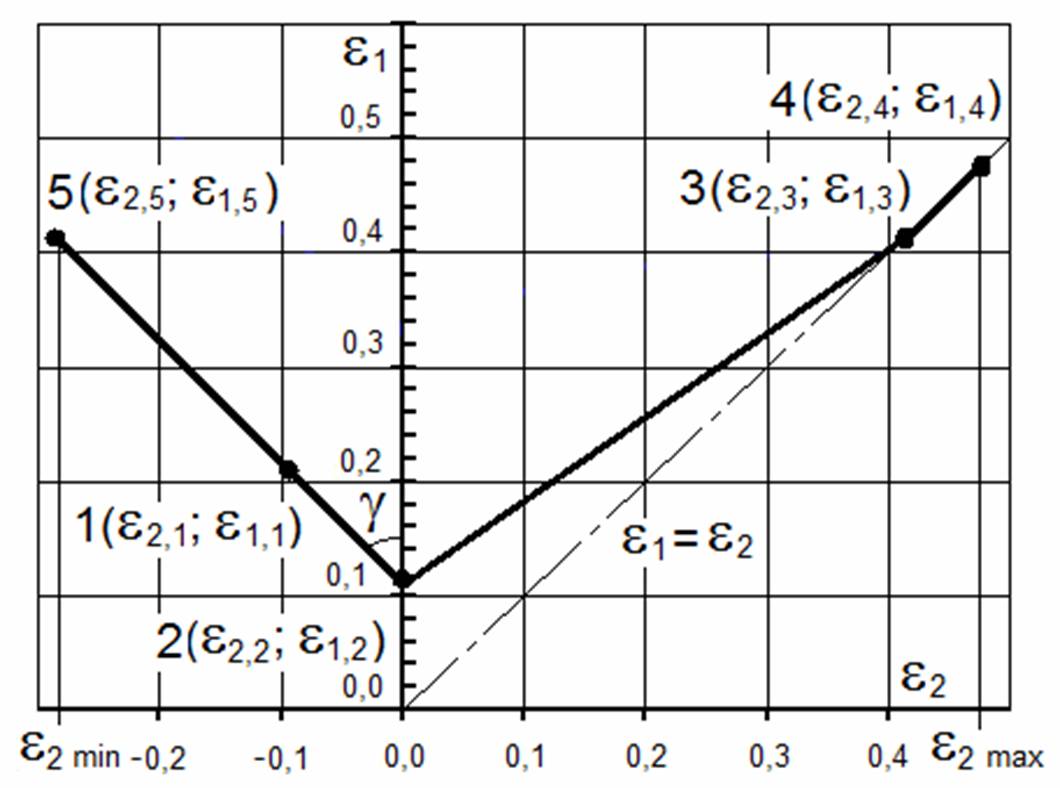
Перед построением ДПД вводят обозначения точки 1(ε_1,1; ε_2,1): деформация в направлении длины l образца ε_p=ε_p,l=ε_1,1=ln(1+δ_p), деформация ε_p,b= ε_2,1=ln(1+δ_b), где δ_b – относительное равномерное сужение по ширине b образца, деформация по толщине s образца ε_p,s=ε_3,1; из условия несжимаемости листового материала ε_1,1+ε_2,1+ε_3,1=0 следует ε_3,1=−ε_1,1−ε_2,1; вторая цифра в индексах означает номер точки на ДПД. Обозначения остальных точек ДПД аналогичны, изменяется только вторая цифра в индексах.

Принимают модель линейного растяжения или сжатия изотропного образца, для которой ε_2,1=ε_3,1=−0,5ε_1,1, и на ДПД строят точку 1(ε_1,1; ε_2,1), рис. 1.

Рис. 1. Метод Жаркова В. А. построения диаграммы предельных деформаций листового материала.

Из точки 1(ε_1,1; ε_2,1) проводят прямую до пересечения с осью ε₁ в точке 2(ε_2,2; ε_1,2); эту прямую проводят под углом γ к оси ординат, который для широко применяемых в автомобильной и других отраслях промышленности листовых материалов равен 45⁰, при этом ε_2,2=0, ε_1,2=0,5ε_1,1. Таким образом полу­чают уравнение левого отрезка прямой ДПД:

ε₁=−ε₂+ε_1,2 или ε₁=−ε₂+0,5ln(1+δ_р) при ε_2,min≤ε₂≤0.

Экспериментально установлено, что при испытании на двухосное растяжение изотропного листового материала, например жидкостью, предельные деформации ε₁ и ε₂ элементов вблизи зоны локального утонения и/или разрушения листового материала равны между собой в два раза больше предельной деформации ε_p=ln(1+δ_p) элементов листового материала при его испытании на одноосное растяжение по ГОСТ 11701-84. Строят точку 3(ε_2,3; ε_1,3) с координатами ε_2,3=2ε_p=2ln(1+δ_р) и ε_1,3=2ε_p=2ln(1+δ_р) и получают уравнение правого отрезка прямой ДПД через две известные точки 2(ε_2,2; ε_1,2) и 3(ε_2,3; ε_1,3):

ε₁=0,75ε₂+0,5ε_1,2 или ε₁=0,75ε₂+0,5ln(1+δ_р) при 0≤ε₂≤ε_2,3.

Из условия ε₁≥ε₂ следует, что правая часть ДПД должна быть выше, касаться или совпадать с прямой ε₁=ε₂. Поэтому из точки 3(ε_2,3; ε_1,3) до точки 4(ε_2,4; ε_1,4) проводят отрезок прямой ДПД с уравнением:

ε₁=ε₂ при ε_2,3≤ε₂≤ε_2,max,

где абсцисса и ордината ε_1,4=ε_2,4=ε_2,max=3ln(1+δ_р) равны с определённым запасом утроенному зна­чению ε_p, поскольку расчётная в CAD/CAE-системах координата ε₂ в элементах листовой заготовки может быть больше ε_2,3.

Отрезок прямой, проходящей через первую и вторую точки, продлевают влево до пятой точки 5(ε_2,5; ε_1,5) с абсциссой ε_2,5=ε_2,min=−ln(1+δ_p), равной с определённым запасом удвоенной координате ε_2,1, поскольку расчётная в CAD/CAE-системах координата ε₂ в элементах листовой заготовки может быть больше ε_2,1.

Построенную по данному методу ДПД вводят в CAD/CAE-систему, например, в систему Marc корпорации MSC Software (США), которая объединяет в себе CAD-программу и CAE-программу, или в программу AutoForm фирмы AutoForm (Швейцария), в виде приведённых выше уравнений или в виде большого количества координат точек, полученных по этим уравнениям. По этим данным CAD/CAE-система строит ДПД в прямоугольной системе координат с заданным масштабом координатной сетки и на эту координатную сетку выводит массив точек с координатами ε₁ и ε₂ всех элементов листовой заготовки на всех этапах её обработки. По номеру и цвету точек определяют те элементы на обрабаты­ваемой листовой заготовке, которые близко расположены (с учётом запаса пластичности) или вышли за ДПД и где велика вероятность разрушения листовой заготовки, и разрабатывают мероприятия по уменьшению вероятности разрушения листовой заготовки в процессе обработки на производстве.

Построенная по данному методу диаграмма предельных деформаций изотропного (ДПДИ) листового материала является первым приближением. Со временем, по мере получения надёжных экспериментальных свойств, например, δ_b по ГОСТ 11701-84 и других свойств, на ДПДИ накладывают диаграмму предельных деформаций анизотропного (ДПДА) листового материала как последующие приближения для реального анизотропного материала, ДПДА вводят в CAD/CAE-систему и более точно, чем с ДПДИ, моделируют и проектируют процесс листовой штамповки, а также при помощи коэффициента анизотропии Жаркова В. А. a_θ [5] (Жарков В. А. Моделирование в системе Marc обработки материалов в машиностроении. Часть 5. Вытяжка осесимметричной детали с утонением стенки. – Вестник машиностроения, 2012, № 12):

 a_θ=(ε₃−ε₂)/(0,5ε₁)100 %,

ε₁=ln(1+δ_р), ε₂=ln(1+δ_b), ε₃=−ε₁−ε₂

для углов θ вырезки образцов по отношению к направлению прокатки листового материала получают качественную и количественную характеристику влияния анизотропии на предельное формоизменение данного листового материла.

Технический результат заключается в том, что, не дожидаясь проведения сложных и дорогостоящих испытаний листового материала на специальной испытательной машине, можно по данному методу быстро построить ДПД на основе только одного стандартного свойства листового материала, а именно, относительного равномерного удлинения δ_р по ГОСТ 11701-84, и использовать эту ДПД как в CAD/CAE-системе, так и на производстве для расчёта вероятности разрушения листовой заготовки на операциях листовой штамповки. Данный метод сокращает время и повышает качество проектирования технологических процессов и оснастки, даёт экономию листового материала за счёт сокращения процента брака при отладке технологических процессов, а также значительно упрощает выбор листового материала и оборудования для листовой штамповки деталей, например, кузовных деталей автомобилей и другой техники.

Вывод

Метод Жаркова В. А. построения диаграммы предельных деформаций листового материала, заключающийся в том, что на полученный из листового материала образец наносят делительную сетку, образец испытывают, измеряют делительную сетку, рассчитывают наименьшую главную деформации ε₂ и наибольшую главную деформацию ε₁ и по нанесённым на координатную сетку значениям деформаций ε₂ по оси абсцисс и ε₁ по оси ординат строят диаграмму предельных деформаций ε₁=f(ε₂), отличающийся тем, что

диаграмму предельных деформаций строят по относительному равномерному удлинению δ_р по ГОСТ 11701-84 "Металлы. Методы испытаний на растяжение тонких листов и лент. Metals. Methods of tensile tests of thin sheets and strips", значение которого берут из нормативно-технической документации на листовой материал, а при отсутствии δ_р проводят только одно испытание на одноосное растяжение образца из листового материала по ГОСТ 11701-84 с целью определения только этого одного свойства δ_р,

затем вычисляют ординату ln(1+δ_p) первой точки диаграммы предельных деформаций, далее для модели линейного растяжения изотропного образца рассчитывают абсциссу −0,5ln(1+δ_p) этой первой точки,

из построенной первой точки проводят отрезок прямой под углом 45⁰ к оси ординат до пересечения с этой осью ординат во второй точке,

третью точку получают с абсциссой и ординатой 2ln(1+δ_р),

соединяют вторую и третью точки отрезком прямой,

из третьей точки проводят отрезок прямой ε₁=ε₂ до четвёртой точки с абсциссой и ординатой 3ln(1+δ_р),

а отрезок прямой, проходящей через первую и вторую точки, продлевают влево до пятой точки с абсциссой −ln(1+δ_p).

Реферат

Метод Жаркова В. А. относится к теории и практике листовой штамповке, а в частности, к исследованию механических свойств листовых материалов для оценки их штампуемости, а также для использования в CAD/CAE-системах при компьютерном моделировании и проектировании формоизменяющих операций листовой штамповки.

Диаграмму предельных деформаций строят по относительному равномерному удлинению δ_р по ГОСТ 11701-84, затем вычисляют ординату ln(1+δ_p) первой точки диаграммы предельных деформаций, далее для модели линейного растяжения изотропного образца рассчитывают абсциссу −0,5ln(1+δ_p) этой первой точки, из построенной первой точки проводят отрезок прямой под углом 45⁰ к оси ординат до пересечения с этой осью ординат во второй точке, третью точку получают с абсциссой и ординатой 2ln(1+δ_р), соединяют вторую и третью точки отрезком прямой, из третьей точки проводят отрезок прямой ε₁=ε₂ до четвёртой точки с абсциссой и ординатой 3ln(1+δ_р), а отрезок прямой, проходящей через первую и вторую точки, продлевают влево до пятой точки с абсциссой −ln(1+δ_p).

Данный метод Жаркова В. А. сокращает время и повышает качество проектирования технологических процессов и оснастки, даёт экономию листового материала за счёт сокращения процента брака при отладке технологических процессов, а также значительно упрощает выбор листового материала и оборудования для листовой штамповки деталей, например, кузовных деталей легковых автомобилей и другой техники. Илл. 1.

Библиографические ссылки

1. Жарков В. А. Моделирование в системе Marc обработки материалов в машиностроении. Часть 1. Одноугловая гибка. – Вестник машиностроения, 2012, № 8, с. 67-72.

2. Жарков В. А. Моделирование в системе Marc обработки материалов в машиностроении. Часть 2. Двухугловая гибка без прижима заготовки. – Вестник машиностроения, 2012, № 9, с. 61-67.

3. Жарков В. А. Моделирование в системе Marc обработки материалов в машиностроении. Часть 3. Двухугловая гибка с прижимом заготовки. – Вестник машиностроения, 2012, № 10.

4. Жарков В. А. Моделирование в системе Marc обработки материалов в машиностроении. Часть 4. Вытяжка осесимметричной детали без утонения стенки. – Вестник машиностроения, 2012, № 11.

5. Жарков В. А. Моделирование в системе Marc обработки материалов в машиностроении. Часть 5. Вытяжка осесимметричной детали с утонением стенки. – Вестник машиностроения, 2012, № 12.

6. Жарков В. А. Моделирование в системе Marc обработки материалов в машиностроении. Часть 6. Вытяжка сложной детали. – Вестник машиностроения, 2013, № 2.

7. Жарков В. А. Моделирование в системе Marc обработки материалов в машиностроении. Часть 7. Испытание и правка растяжением. – Вестник машиностроения, 2013, № 3.

8. Жарков В. А. Visual C# 2012 в учёбе, науке и технике. – М.: Издательство "Жарков Пресс", 2013. – 818 страниц с компакт-диском (www.ZharkovPress.com).

9. Жарков В. А. Статьи во всех номерах журнала "Кузнечно-штамповочное производство", начиная с 2010 года (www.ZharkovPress.com).

Метод Жаркова В. А. построения диаграммы деформирования заготовки с учётом упрочнения

Method by Zharkov V. A. of construction of deformation diagram of blank into account hardening

Кривые упрочнения материала строятся по данным, получаемым, например, из испытаний образцов на одноосное растяжение или сжатие (осадку). Если в этих испытаниях в образце имеет место линейное напряжённо-деформированное состояние (НДС), то напряжение текучести σ_s определяется как частное от деления силы деформирования F на истинную площадь поперечного сечения образца A на данном этапе деформирования.

Кривыми упрочнения пользуются для анализа характера и степени влияния упрочнения на НДС и величину необходимых для деформирования сил при математическом моделировании обработки заготовок. Для аналитического решения задачи по установлению влияния упрочнения на величину силы деформирования и распределение напряжений и деформаций в обрабатываемой заготовке необходимо кривую упрочнения представить в виде уравнения, связывающего напряжение текучести с деформациями. В теории пластичности применяют несколько основных функциональных зависимостей напряжения текучести или σ_s от интенсивности деформаций ε_i, которые рассмотрены во многих книгах, например, в наших книгах с сайта ZharkovPress.com.

Во всех книгах и статьях Жаркова В. А., а также в патентах с участием Жаркова В. А. при теоретическом исследовании процессов обработки материалов давлением (ОМД), а также при математическом моделирования ОМД на основе какой-либо CAD/CAE-системы (Computer-Aided-Design/Computer-Aided-Engineering-system), например, системы Marc корпорации MSC Software, мы будем использовать авторскую методику Жаркова В. А. построения диаграммы деформирования заготовки с учётом упрочнения; эта методика с высокой точностью соответствует реальному процессу деформирования.

С целью расчёта упрочнения каждого элемента (узла, точки или частицы) заготовки, который перешёл в пластическое состояние на каком-то этапе обработки этой заготовки, принимаем, что напряжение текучести σ_s элементов в пластическом состоянии всегда равно интенсивности напряжений σ_i (согласно условию пластичности) и в зависимости от интенсивности деформаций ε_i с учётом упрочнения заготовки определяется по формуле Жаркова В. А.:

σ_s = σ_т + σ_в(1 + δ_р)ε_iⁿ,  

где σ_s – увеличивающийся за счёт упрочнения предел текучести пластически деформируемого элемента обрабатываемой заготовки, называемый как напряжение текучести, на каждом этапе обработки заготовки равное (по условия пластичности) интенсивности напряжений σ_i, иначе, эквивалентному (equivalent), обобщённому или эффективному напряжению;

σ_т – предел текучести физический (если на диаграмме растяжения образца имеется площадка текучести) или предел текучести условный σ_0,2 (для остаточного относительного удлинения образца 0,002 или 0,2%) по ГОСТ 11701-84 "Металлы. Методы испытаний на растяжение тонких листов и лент. Metals. Methods of tensile tests of thin sheets and strips";

σ_в – предел прочности, иначе, временное сопротивление по ГОСТ 11701-84;

σ_{в true} или σ_в,t = σ_в(1 + δ_р) – истинный предел прочности (термин Жаркова В. А.);

δ_р – относительное равномерное удлинение по ГОСТ 11701-84;

n – показатель степени упрочнения, который определяем по следующей методике.   

При стандартном испытании на растяжение плоского образца по ГОСТ 11701-84 с исходными размерами s₀, b₀, l₀ (s₀ – толщина, b₀ – ширина, l₀ – длина) в момент начала образования шейки на образце (когда начинается локальное утонение образца, а сила растяжения максимальна и равна F_max) размеры образца равны s_u, b_u, l_u. Показатель степени упрочнения n определяется по формуле Жаркова В. А. σ_s = σ_т + σ_в,t ε_iⁿ из условия, что в этот момент начала образования на образце шейки напряжение текучести σ_s равно истинному пределу прочности σ_в,t:

σ_s = σ_в,t = σ_в(1 + δ_р),

 где предел прочности равен σ_в=F_max/(s₀b₀), а относительное равномерное удлинение равно δ_p=(l_u - l₀)/l₀ на расчётной длине образца (если испытание останавливают в момент начала образования на образце шейки) или на части расчётной длины образца на участке с равномерным удлинением образца (если при испытании образец доводят до разрыва).

Предел текучести физический или σ_т или предел текучести условный σ_0,2, предел прочности σ_в и относительное равномерное удлинение δ_р определяются по ГОСТ 11701-84 и ГОСТ 1497-84. Интенсивность деформаций ε_i рассчитывается по формуле

ε_i = [2/√(3)]√ (ε₁² + ε₁ε₂ + ε₂²)

и в этот же момент (начала образования шейки на образце) равна величине ε_i,u, если в последнюю формулу подставить значения

 ε₁ = ε_Р = lnδ_p = ln[(l_u - l₀)/l₀] и ε₂ = ε_b = lnδ_b = ln[(b_u - b₀)/b₀].

Для наиболее часто применяемой расчётной модели линейного растяжения или сжатия изотропного образца имеем ε₂ = -0,5ε₁ и после подстановки в формулу для интенсивности пластических деформаций ε_i получаем:

ε_i,u = ε_Р = ln(1 + δ_p) = ln[1 + (l_u - l₀)/l₀].

Таким образом, для момента начала образования на образце шейки формула Жаркова В. А. σ_s = σ_т + σ_в,t ε_iⁿ принимает вид формулы:

σ_в(1 + δ_р) = σ_т + σ_в(1 + δ_р)[ln(1 + δ_p)]ⁿ,

после логарифмирования которой получаем формулу Жаркова В. А. для расчёта показателя степени деформационного упрочнения заготовки:

n = ln{1−σ_т/[σ_в(1+δ_р)]}/ln[ln(1+δ_р)].

Отметим, что при поэтапном исследовании обработки заготовки для первого этапа напряжение текучести σ_s во всех конечных элементах заготовки принимается одинаковым и равным σ_т. На последующих этапах деформирования величина σ_s становится переменной для различных конечных элементов заготовки в зависимости от интенсивности накопленных пластических деформаций, и эта величина σ_s будет рассчитываться по формуле Жаркова В. А. σ_s = σ_т + σ_в(1 + δ_р)ε_iⁿ.

Для примера, далее в наших книгах с сайта ZharkovPress.com, например, в книге "Жарков В. А. Теория Жаркова В. А. листовой штамповки", мы построим диаграмму деформирования для широко применяемой в промышленности низкоуглеродистой стали 08Ю ОСВ по ГОСТ 9045-93 "Прокат тонколистовой холоднокатаный из низкоуглеродистой качественной стали для холодной штамповки. Технические условия. Cold-rolled thin sheets of low-carbon steel for cold stamping. Specification" толщиной 1,2 мм со следующими механическими свойствами, полученными после стандартных испытаний образцов на растяжение: предел текучести σ_0,2 = 190 Н/мм² (для остаточного относительного удлинения образца 0,002 или 0,2 % по ГОСТ 1497-84, см. рисунок выше), предел прочности σ_в = 305 Н/мм² и относительное равномерное удлинение δ_р = 0,231.

Коэффициент анизотропии Жаркова В. А.

Zharkov's anisotropy coefficient

Для линейного растяжения изотропного материала (у которого все свойства одинаковы для всех углов θ вырезки образцов по отношению к направлению прокатки) справедливо основное равенство: ε_b,p=ε_s,p=−0,5ε_l,p. Поэтому для количественной оценки анизотропии материала д.т.н. Жарковым В. А. предложен [1] новый коэффициент анизотропии Z_θ, где буква Z является первой буквой слова Zharkov - фамилии автора этого нового коэффициента анизотропии

(защищённого патентами Российской Федерации 2655634, 2655636, 2659458):

            Z_θ=(ε_s,p−ε_b,p)/(0,5ε_l,p)

или в процентах:

    Z_θ=(ε_s,p− ε_b,p)/(0,5ε_l,p)*100%,             

где ε_l,p, ε_b,p, ε_s,p - логарифмические равномерные деформации по длине l, ширине b и толщине s в момент окончания равномерного удлинения и начала образования на образце шейки по ГОСТ 11701-84 "Металлы. Методы испытаний на растяжение тонких листов и лент".

        Из условия несжимаемости металла следует: ε_l,p+ε_b,p+ε_s,p=0 или ε_s,p=-ε_l,p-ε_b,p.

        Логарифмическая равномерная деформация по длине l равна ε_l,p=ln(1+δ_р), где δ_р=δ_l,p- относительное равномерное удлинение по ГОСТ 11701-84.

        По ГОСТ 11701-84 коэффициент анизотропии равен R_a=ln(b_р/b₀)/ln(s_р/s₀)=ln(b_р/b₀)/ln[l₀b₀/(l_рb_р)], откуда находим логарифмическую деформацию по ширине образца

        ε_b,p=ln(b_p/b₀)=−R_a/(1+R_a)ln(1+δ_l,p)  

для испытания на растяжение образца с исходными расчётными размерами s₀, b₀, l₀ (s₀ – толщина, b₀ – ширина, l₀ – начальная расчётная длина).

        Отличие коэффициента Жаркова Z_θ от R_a по ГОСТ 11701-84 заключается в том, что для изотропного материала (при нулевой анизотропии) коэффициент R_a равен единице, а коэффициент Жаркова Z_θ равен нулю, что более логично.

        Чем больше (по абсолютной величине) Z_θ для заданного угла θ, тем больше степень анизотропии материала.

        Если Z_θ имеет положительное значение, деформация по ширине образца превалирует над деформацией по толщине и наоборот.

        Если Z_θ одинаков в плоскости листа, но отличен от нуля, такую анизотропию называют нормальной (к плоскости листа) анизотропией.

        Если Z_θ различен в плоскости листа, такую анизотропию называют плоскостной.

        Например, для оцинкованной стали 01ЮТ ВОСВ ГЦ по ТУ 14-105-685-2002 толщиной 0,7 мм при θ=90^о, Z_θ=Z₉₀=0,921, анизотропия листа очень большая, что необходимо учитывать при проектировании технологии изготовления деталей из этого листа.

Литература

1. Жарков В. А. Моделирование в системе Marc обработки материалов в машиностроении. Часть 1, 2, 3, 4, 5, 6, 7. – Вестник машиностроения, 2012, № 8, 9, 10, 11, 12; 2013, № 2, 3.

2. Жарков В. А. Испытания материалов. Анизотропия листов и её влияние на листовую штамповку. - Вестник машиностроения, 2017, № 11, с. 46-55.

Основные определения напряжённо-деформированного состояния обрабатываемой заготовки

The basic definitions of stressed-deformed condition of processed blank

Для понимания механизма формоизменения заготовки и распределения полей перемещений, деформаций и напряжений в элементах заготовки приведём основные определения напряжённо-деформированного состояния (НДС) заготовки применительно к обработке материалов давлением (ОМД), в частности, к вытяжке листового материала.

В процессе обработки элементы заготовки характеризуются такой векторной величиной, как перемещение, и такими тензорными величинами, как деформации и напряжения. Интенсивность напряжений σ_i, иначе называемая как эквивалентное напряжение (Equivalent Stress), эффективное напряжение или обобщённое напряжение, в главных напряжениях σ₁, σ₂, σ₃, действующих из координатных плоскостей, в которых касательные напряжения равны нулю, рассчитываем по формуле

σ_i = [1/√(2)]√[(σ₁ - σ₂)² + (σ₂ – σ₃)² + (σ₃ - σ₁)²],

где √  – знак квадратного корня, причём подкоренное выражение находится внутри тех двух скобок, тип которых определён первой скобкой за знаком корня.

Для принятой нами расчётной модели плоского (при σ₃ = 0) напряжённого состояния листовой заготовки в процессе обработки интенсивность напряжений σ_i рассчитываем по формуле

σ_i = √(σ₁² − σ₁σ₂ + σ₂²),

где σ₁ или σ_r – наибольшее главное растягивающее радиальное (вдоль радиуса заготовки) напряжение; σ₂ или σ_t – наименьшее (не по модулю, а с учётом знака "-") главное сжимающее окружное (перпендикулярно радиусу заготовки) или тангенциальное напряжение; третье среднее по значению главное напряжение σ₃ или σ_q в направлении толщины заготовки принимаем равным или близким к 0, так как сила прижима фланца заготовки во много раз меньше предела текучести заготовки. Главные напряжения σ₁, σ₂, σ₃ действуют из координатных плоскостей шестигранного элемента, в которых касательные напряжения равны нулю. Интенсивность напряжений σ_i, как и сами напряжения σ₁, σ₂, σ₃, измеряется в Н/мм².

Часто, например в системе Marc корпорации MSC Software (США), напряжённое состояние исследуется на основе безразмерной величины, равной отношению интенсивности напряжений σ_i, иначе называемой как эквивалентное напряжение (Equivalent Stress), к пределу текучести σ_T, иначе называемому как Yield Stress (Equivalent Stress/Yield Stress): σ_i /σ_T.

В процессе обработки элементы фланца заготовки, переходящие сначала на кромку матрицы и далее в стенку вытягиваемой детали, накапливают всё больше пластических деформаций с интенсивностью ε_i, за счёт этого всё больше упрочняются, и их изменяемый предел текучести, теперь называемый напряжением текучести σ_s, также всё больше увеличивается. И чтобы поддерживать эти элементы в пластическом состоянии, требуется всё большая энергия или интенсивность напряжений σ_i в этих элементах, создаваемая инструментами штампа и работой прессового оборудования (на котором установлен штамп).

Для расчёта деформаций элементов заготовки используем уравнения для компонентов тензора приращений деформаций, а именно, для главной радиальной dε_r (или dε₁) и главной тангенциальной dε_t (или dε₂) деформаций

dε_r = d(∆u)/dr,   dε_t = ∆u/r,

где ∆u – приращение радиального перемещения элемента заготовки текущего радиуса r на данном j-м этапе обработки заготовки.

Приращение интенсивности пластических деформаций dε_i элементов на каждом этапе обработки заготовки рассчитываем по формуле

dε_i = [2/√(3)]√(dε₁² + dε₁dε₂ + dε₂²),

где √ – знак квадратного корня, причём подкоренное выражение находится внутри тех двух скобок, тип которых определён первой скобкой за знаком корня.

Полная (накопленная) интенсивность деформаций ε_i в любом элементе заготовки на j-м этапе обработки, например, при j=N складывается из приращений интенсивности деформаций для всех предыдущих j-х этапов.

Если для расчёта деформаций элементов заготовки на данном j-м этапе обработки мы используем уравнения для компонентов тензора не приращений, а полных накопленных за все предыдущие этапы обработки деформаций, а именно, главной радиальной деформации  ε_r (или ε₁), главной тангенциальной деформации ε_t (или ε₂) и главной деформации ε_s (или ε₃) в направлении толщины заготовки, действующих из координатных плоскостей шестигранного элемента, в которых деформации сдвига равны нулю, то интенсивность пластических деформаций ε_i элементов на каждом этапе обработки заготовки рассчитываем по формуле

ε_i = {[√(2)]/3}√ [(ε₁ - ε₂)² + (ε₂ – ε₃)² + (ε₃ – ε₁)²].

С учётом условия не­сжимаемости материала при пластическом деформировании ε₁+ε₂+ε₃=0 следует ε₃=−ε₁−ε₂, и предыдущая формула принимает окончательный вид

ε_i = [2/√(3)]√ (ε₁² + ε₁ε₂ + ε₂²).

В базовом случае, для идеализированной расчётной схемы линейного растяжения (или сжатия) изотропного материала

ε₂ = ε₃ = −0,5ε₁, ε_i = ε₁, σ_i = σ₁,

где ε₁ – наибольшая главная деформация, а σ₁ – наибольшее главное растягивающее (или сжимающее) напряжение в материале в направлении действия силы от обрабатывающего инструмента.

Строго говоря, как и компоненты тензора деформаций, полная или суммарная интенсивность деформаций ε_i равна сумме интенсивности упругих деформаций ε_i,e и интенсивности пластических деформаций ε_i,p:        

ε_i = ε_i,e + ε_i,p.

По закону теории пластичности, упругие деформации всегда сопровождают пластические деформации. Но поскольку в моделируемых нами формоизменяющих операциях листовой штамповки интенсивность пластических деформаций ε_i,p в опасном (с точки зрения разрушения) сечении штампуемой заготовки во много раз больше интенсивности упругих деформаций   ε_i,e, то часто под полной интенсивностью деформаций мы будем понимать интенсивность пластических деформаций или короче интенсивность деформаций ε_i. И только в особых случаях при исследовании, например, упругого пружинения отштампованной детали под воздействием остаточных напряжений, мы будем рассматривать и учитывать в расчётах компоненты тензора и интенсивность упругих деформаций.

Напряжение текучести σ_s элементов в пластическом состоянии всегда равно интенсивности напряжений σ_i (согласно условию пластичности) и в зависимости от интенсивности деформаций ε_i с учётом упрочнения заготовки мы будем задавать по формуле Жаркова В. А.:

σ_s = σ_т + σ_в,t ε_iⁿ,   n = ln{1−σ_т/[σ_в(1+δ_р)]}/ln[ln(1+δ_р)],

где предел текучести физический σ_т (если на диаграмме растяжения образца имеется площадка текучести) или предел текучести условный σ_0,2 (для остаточного относительного удлинения образца 0,002 или 0,2%), предел прочности σ_в, истинный предел прочности σ_{в true} или σ_в,t=σ_в(1+δ_р) и относительное равномерное удлинение δ_р определяем по ГОСТ 11701-84 "Металлы. Методы испытаний на растяжение тонких листов и лент. Metals. Methods of tensile tests of thin sheets and strips".

Теория Жаркова В. А. осесимметричной вытяжки детали из листовой заготовки

The short theory by Zharkov V. A. of axisymmetric deep drawing the detail from sheet blank

Воспользуемся приведёнными выше основными определениями напряжённо-деформированного состояния обрабатываемой заготовки для создания краткой теории Жаркова В. А. осесимметричной вытяжки детали без фланца среднего диаметра d стенки детали (среднего между диаметром у дна и края срединной поверхности стенки детали) из плоской круглой листовой заготовки диаметра D₀ (или радиуса R₀). Более подробная теория Жаркова В. А. осесимметричной вытяжки будет приведена далее.

На каждом этапе обработки заготовки по мере удаления от контура внутрь заготовки радиальное растягивающее напряжение σ_r увеличивается, а тангенциальное сжимающее напряжение σ_t уменьшается (что следует из условия пластичности), вследствие чего увеличенная на контуре заготовки толщина также уменьшается по мере удаления от контура внутрь заготовки.

На каждом этапе обработки заготовки по мере удаления от контура внутрь заготовки радиальное растягивающее напряжение σ_r увеличивается, а тангенциальное сжимающее напряжение σ_t уменьшается (что следует из условия пластичности), вследствие чего увеличенная на контуре заготовки толщина также уменьшается по мере удаления от контура внутрь заготовки, и на фланце имеется прилегающая к контуру заготовки зона утолщения и прилегающая к кромке матрицы зона утонения. Но даже на внутреннем контуре плоского фланца заготовки и далее на закруглении кромки матрицы сжимающее напряжение σ_t остаётся достаточно большим, чтобы вызвать потерю устойчивости на этих участках заготовки. В частности, первый тип потери устойчивости с образованием складок происходит на краевых участках заготовки либо под прижимом при небольшой силе прижима, либо на вышедших в процессе вытяжки из-под прижима штампа участках заготовки, что мы и увидим далее.

На j-м этапе при увеличении толщины от s₀ до s_j и смещении от R₀ до R_j на краю заготовки, где σ_r = 0, σ_z ≈ 0 и логарифмические деформации ε_z = ln(s_j/s₀), ε_t = ln(R_j/R₀) , имеет место линейное сжатие ε_r = ε_z = -1/2ε_t, и из последних двух уравнений получаем

s_j = s₀ √(R₀/R_j),

где σ_z и ε_z – напряжение и деформация в направлении толщины заготовки.

После втягивания от R₀ до R_pm=(R_p+R_m)/2 всего фланца в зазор между пуансоном радиуса R_p и матрицей внутреннего радиуса R_m конечная толщина края вытянутой детали приближённо равна 

s_k = s₀√(R₀/R_pm) = s₀√K,

где K – коэффициент вытяжки, равный отношению диаметра заготовки D₀ = 2R₀ к среднему диаметру стенки детали d, который без учёта пружинения стенки вытянутой детали после выталкивания из матрицы равен (на основании размеров пуансона и матрицы)  d = 2R_pm.

Распределение напряжений σ_r, σ_t вдоль радиуса r фланца заготовки можно определить аналитически, решая совместно уравнение равновесия

dσ_r/dr + (σ_r - σ_t)/r = 0

и уравнение пластичности

σ_r - σ_t = σ_s.

После подстановки последнего уравнения в предпоследнее и интегрирования с учётом граничного условия, что при r = R_j, σ_r = 0, получаем

σ_r = σ_s ln(R_j/r).

Зная σ_r, напряжение σ_t находим из уравнения пластичности. Из уравнения связи напряжений и накопленных за все j-е этапы деформаций

σ_r / σ_t = (ε_r – ε_z)/(ε_t - ε_z)

можно найти поле деформаций.

Радиус r_s0,j, разграничивающий зону утолщения фланца от зоны утонения, можно установить, подставляя r = r_s0,j в уравнение σ_r = σ_s ln(R_j/r_s0,j) и уравнение пластичности σ_t = σ_r - σ_s и используя условие плоского деформированного состояния элементов на этом радиусе (σ_r + σ_t)/2 = σ_z при σ_z ≈ 0 и σ_r + σ_t ≈ 0. В итоге, на j-м этапе:

r_s0,j = R_j/√e ≈ 0,607R_j.

Некоторые библиографические ссылки из более чем 100 публикаций Жаркова В. А. в России и за рубежом

1. Жарков В. А. Моделирование в системе Marc обработки материалов в машиностроении. Часть 1. Одноугловая гибка. – Вестник машиностроения, 2012, № 8, с. 67-72.

2. Жарков В. А. Моделирование в системе Marc обработки материалов в машиностроении. Часть 2. Двухугловая гибка без прижима заготовки. – Вестник машиностроения, 2012, № 9, с. 61-67.

3. Жарков В. А. Моделирование в системе Marc обработки материалов в машиностроении. Часть 3. Двухугловая гибка с прижимом заготовки. – Вестник машиностроения, 2012, № 10, с. 60-66.

4. Жарков В. А. Моделирование в системе Marc обработки материалов в машиностроении. Часть 4. Вытяжка осесимметричной детали без утонения стенки. – Вестник машиностроения, 2012, № 11, с. 58-65.

5. Жарков В. А. Моделирование в системе Marc обработки материалов в машиностроении. Часть 5. Вытяжка осесимметричной детали с утонением стенки. – Вестник машиностроения, 2012, № 12, с. 54-61.

6. Жарков В. А. Моделирование в системе Marc обработки материалов в машиностроении. Часть 6. Вытяжка сложной детали. – Вестник машиностроения, 2013, № 2, с. 67-73.

7. Жарков В. А. Моделирование в системе Marc обработки материалов в машиностроении. Часть 7. Испытание и правка растяжением. – Вестник машиностроения, 2013, № 3, с. 43-48.

8. Жарков В. А. Visual C# 2014 в учёбе, науке и технике. – М.: Издательство "Жарков Пресс", 2014. – 818 страниц с компакт-диском (www.ZharkovPress.com).

9. Жарков В. А. Статьи во всех номерах журнала "Кузнечно-штамповочное производство", издаваемого д.т.н. Жарковым В. А. начиная с 2010 года (www.ZharkovPress.com).

Журнал "Кузнечно-штамповочное производство" зарегистрирован в Роскомнадзоре: Свидетельство о регистрации средства массовой информации ПИ № ФС77-35975 от 20 апреля 2009 г.

Данный журнал "Kuznečno-štampovočnoe proizvodstvo (Moskva)"  7 октября 2009 года получил международный стандартный сериальный номер (International Standard Serial Number) ISSN 2076-4448.

Книги и статьи д.т.н. Жаркова В. А.

Д.т.н. Жарков В. А. опубликовал самое большое количество книг, статей и патентов среди всех специалистов в области обработки материалов давлением, а именно: более 100 книг, статей и патентов в отечественных и зарубежных издательствах, вот некоторые из них.

Книга в Англии:

Zharkov V. A. Theory and Practice of Deep Drawing. – London, Mechanical Engineering Publications Limited, 1995. – 601 pages.

Книга в России: 

Жарков В. А.Visual C++ на практике. М.: Издательство "Лаборатория Базовых Знаний", 2002. – 424 с: ил.

Более 30 книг, опубликованные Жарковым В. А. в собственном издательстве 000 "Издательство "Жарков Пресс" и представленные на сайте издательства www.ZharkovPress.com, например:

Жарков В. А. Теория Жаркова В. А. листовой штамповки. – М.: Издательство "Жарков Пресс", 2016. – 968 страниц с видео-диском.

Жарков В. А. Компьютерное моделирование штамповки материалов  в системе Marc корпорации MSC Software (США). – М.: Издательство "Жарков Пресс", 2016. – 927 страниц с видео-диском.

Жарков В.А. Программирование на Visual C# задач в учёбе, науке и технике. – М.: Издательство "Жарков Пресс", 2016. – 818 страниц с видео-диском.

Серии статей, опубликованные за рубежом, например, серия из 10 статей в главном итальянском журнале по штамповке Lamiera:

Zharkov V.A. Metodologia di sviluppo rapido di sistemi Cad/Cam. Lamiera (Italy), 2002, n.9, 178-183; 2003, n.3, 158-166; 2003, n. 4, 194-200; 2003, n. 9, 194-206; 2003, n. 11, 158-169; 2004, n. 3, 114-123; 2004, n. 6, 116-127; 2004, n. 7, 96-107; 2004, n. 8, 98-104; 2005, n. 3.

Серии статей, опубликованные в отечественных журналах, например, серия из 7 статей в главном российском техническом журнале "Вестник машиностроения":

Жарков В. А. Моделирование в системе Marc обработки материалов в машиностроении. Части 1, 2, 3, 4, 5, 6, 7. – Вестник машиностроения, 2012, № 8, 9, 10, 11, 12; 2013, № 2, 3.

Продолжение следует.